Index
Index
- 의사결정나무(Decision Tree)는 뭘까?
- 의사결정나무의 철학: Information Gain
- 의사결정나무의 종류 : Type of Tree
- 의사결정나무의 학습과정: Learning Process
- sklearn 라이브러리를 활용한 의사 결정나무
- 참고자료
 의사결정나무(Decision Tree)는 뭘까?
의사결정나무(Decision Tree)는 뭘까?
의사결정나무란 데이터 사이 존재하는 패턴 을 찾아 이 규칙들의 조합 으로 예측 모델을 만드는데 쓰이는 알고리즘으로 기계학습의 기초가 되는 알고리즘 중 하나이다.
그림으로 그렸을때 트리의 형태를 이루기 때문에 ‘나무’ 라는 말이 붙었는데 이는 추후 여러 의사결정나무를 앙상블 기법을 통해 활용한 Random Forest 알고리즘에도 영향을 주었다.
의사결정나무는 설명변수를 *하나씩만* 활용하여 가지뻗기를 진행하는데 이는 우리가 어릴적 한번씩 해봤던 ‘스무고개’ 놀이를 통해 이해할 수 있다.
의사결정나무에 대한 설명을 보면
설명변수라는 용어가 쓰이는데입력특성,독립변수정도로 이해하면 된다.

다음과 같은 스무고개 놀이를 했을 때 다리 ,고양이와 크기가 비슷 , 바다에 사는 은 모두 위에서 언급한 설명변수에 해당한다. 데이터에 대한 패턴을 찾아 트리 구조로 규칙을 조합해놓은 모양이다. 한번에 설명변수 하나씩만을 이용해 가지를 뻗게되어 terminal node , leaf node 라고 부르는 트리의 최하위 항목들을 살펴보면 초기 데이터의 상호 베타적인 집합으로 분류되어 있는것을 확인할 수 있다.
의사결정나무는 이런 모양으로 규칙을 조합하여 데이터에 대한 예측 모델을 이룬다. 이는 분류(Classification) 문제와 회귀(Regression) 문제 모두 적용가능한데 , 분류 문제의 경우 해당 데이터가 최종적으로 속한 최하위 그룹의 최빈값을 예측값으로 활용하고 회귀 문제의 경우 그 그룹내 데이터의 평균값을 예측값으로 활용한다.즉, N개의 최하위 노드를 갖는 의사결정나무로부터 얻을 수 있는 예측값의 종류는 분류|회귀 문제와 상관없이 동일하게 최대 N개이다.
 의사결정 나무의 철학: Information Gain
의사결정 나무의 철학: Information Gain
앞에서 언급한 스무고개 놀이를 하는데 만약 첫 질문에 ‘혹시 매운 음식인가요?’ 라고 물었는데 ‘네’ 라는 결과가 나온다면 우리는 ‘나이스!’ 를 외칠것이다. 왜일까?
이는 우리가 고려해야하는 정답 후보 데이터가 아주 세부적으로 바뀌었기 때문이다. 의사결정나무에서는 이를 정보획득(Information Gain) 이라 부른다. 정확한 의미는 의사결정나무에서 분기가 일어날때 데이터의 순도 변화량을 정보획득이라 부른다. 데이터의 순도(homogeneity) 란 말 그대로 데이터가 얼마나 단조로운/변화가 많은 혹은 종류가 적은/많은가 정도로 이해하면 되는데 이와 반대되는 개념으로 불순도(impurity) 를 통해 정보획득을 분기 전후의 불순도 감소정도로 설명하기도 한다.
방금 정보획득을 순도의 증가량 , 불순도의 감소량 이라는 표현을 통해 설명하였는데 그러면 이는 수치적으로 어떻게 표현될까?
순도,불순도를 수치로 나타내기 위한 종류는 대표적으로 3가지가 있다. 바로 Entropy , Gini Index , Misclassification Error 인데, 이 중 Entropy 지표에 대해 알아보자면 다음과 같은 식으로 정의된다.
초기 m 개의 분류를 가진 데이터에 대해서는 위의 식 처럼 각 분류의 확률과 확률의 로그값을 모두 더한 값이 초기 엔트로피 값이다. 이 상태에서 데이터나 나뉘게 되면 다음과 같은 방식으로 엔트로피를 구하게 된다.
각 나뉜 각 그룹에 대해 엔트로피를 구한 다음 그룹의 상대 부피인 R 값을 곱하여 다시 더하는 식이다.
의사결정나무의 학습방법에서 핵심은 저 엔트로피 지수가 낮아지는 쪽으로 분기를 하는것이다.
 의사결정나무의 종류 : Type of Tree
의사결정나무의 종류 : Type of Tree
위에서 언급한 3가지 대표 지표 외에도 불순도를 측정하는 다양한 척도와 계산 법이 존재하는데 이는 종속변수의 성격이 연속형인지 범주형인지에 따라 나뉘며 이에 따라 다양한 형태의 의사결정나무가 존재한다. 아래는 각 형태의 간략한 설명이다. 가장 많이 쓰이고 있는 모델은 CART 모델이다.
| 범주형 종속변수 | 연속형 종속변수 | |
|---|---|---|
| CHAID | 카이제곱 통계량 | ANOVA F-통계량 |
| CART | 지니지수 | 분산감소량 |
| C4.5 | 엔트로피지수 |
-
CART (Classification and Regression Tree)
- 가장 널리 쓰이는 의사결정나무 알고리즘. 범주형 종속변수에 대해서는 지니지수를 기준으로 분기가 일어나고 연속형 종속변수에 대해서는 분산을 활용한 이진분리가 기준이 된다.

- 가장 널리 쓰이는 의사결정나무 알고리즘. 범주형 종속변수에 대해서는 지니지수를 기준으로 분기가 일어나고 연속형 종속변수에 대해서는 분산을 활용한 이진분리가 기준이 된다.
-
C4.5
- 각 노드에서 다중분리(multiple split)가 가능하다는 것이 특징이다. 범주형 종속변수의 학습에만 활용되는 알고리즘으로 엔트로피 지수를 통해 분기가 일어난다.
-
CHAID (CHi-sqaured Automatic Interaction Detection)
- 다른 알고리즘과 달리
*Full Tree를 만족할 때까지 분기가 일어나지 않고 적당한 크기에서 분기를 중단하는것이 특징이다. 분기 기준으로는 카이제곱 통계량을 활용하고 독립변수는 범주형 데이터여야 한다는 특징 또한 가지고 있다.
- 다른 알고리즘과 달리
*Full Tree : 모든 leaf_node 의 순도가 100% 인 나무 모델을 말한다.
 의사결정나무의 학습과정 : Learning Process
의사결정나무의 학습과정 : Learning Process
의사결정나무의 학습과정은 신경망 모델의 1회 학습과정과 시각적으로 유사하다. 2 단계를 거쳐 모델이 생성되는데 바로 재귀적 분기(recursive partitioning) 와 가지치기(pruning) 이다.
계산과정과 함께 이해하기 위해 다음과 같은 샘플 데이터를 생각해보자.
| A(독립) | B(독립) | C(종속) |
|---|---|---|
| 16.6 | 2 | YES |
| 5.4 | 3 | NO |
| 20 | 3 | YES |
| 43.6 | 3 | YES |
| 5 | 2 | NO |
| 12 | 3 | YES |
| 12.7 | 2 | NO |
| 17.5 | 2 | NO |
A,B 의 독립 변수에 의해 C의 종속변수 값이 정해지는 데이터일때,
1. 재귀적 분기 (Recursive Partitioning)
먼저 해당 데이터에 대해 분기가 일어난다.
초기 엔트로피 값은
YES : -(4/8) * (log(4/8)) = 0.5
NO : -(4/8) * (log(4/8)) = 0.5
로 0.5 + 0.5 = 1 이다. (엔트로피 지수에서 최대 값이 1이다. 즉 가장 불순도가 높은 유형이 범주 수만큼 나뉘어 있는 데이터)
이때 , 독립 변수 하나를 고정하여 그 값으로 정렬을 한다. (A 기준이라면)
| A(독립) | B(독립) | C(종속) |
|---|---|---|
| 5 | 2 | NO |
| 5.4 | 3 | NO |
| 12 | 3 | YES |
| 12.7 | 2 | NO |
| 16.6 | 2 | YES |
| 17.5 | 2 | NO |
| 20 | 3 | YES |
| 43.6 | 3 | YES |
정렬이 끝나면 총 8개의 데이터가 위에서부터 1:7 , 2:6 , 3:5 , … 의 비율로 분기될때 엔트로피를 계산하여 정보획득을 계산한다.
ex) 1:7
1 : 1/8(데이터 비율) * {-1*log(1)} = 0 (데이터가 한 범주에 대해서만 존재하므로)
| A(독립) | B(독립) | C(종속) |
|---|---|---|
| 5 | 2 | NO |
2 : 7/8(데이터 비율) * {-4/7 * log(4/7) + -3/7 * log(3/7)} (각각 YES , NO 데이터 항목) ≒ 0.5649
| A(독립) | B(독립) | C(종속) |
|---|---|---|
| 5.4 | 3 | NO |
| 12 | 3 | YES |
| 12.7 | 2 | NO |
| 16.6 | 2 | YES |
| 17.5 | 2 | NO |
| 20 | 3 | YES |
| 43.6 | 3 | YES |
분기 후 엔트로피 = 0 + 0.5649 = 0.5649
∴ 정보 획득 = 1 - 0.5649 = 0.4251
위와 같은 작업을 모든 독립변수 에 대해서 모든 비율 로 분기될때를 계산하여 가장 정보획득이 가장 큰 조건을 택해 분기하는 것이다.
wow ! 난 여기서 가장 와닿았다.
그럼 그 다음 분기는 어떻게 일어날까?
예를 들어 위 데이터가 A 변수를 위에서부터 3:5 로 분할하여 분기할때 가장 정보획득이 커 Left 그룹과 Right 그룹으로 나누었다고 하자. 그럼 이후에는 Left 그룹의 3개 데이터로 모든 최하위 그룹이 순수 노드가 될때까지 즉, ‘YES’ 혹은 ‘NO’ 의 데이터만 가지고 있는 그룹이 될 때까지 Left - Left , Left - Right , … 나누고 작업이 끝나면 처음 나누었던 Right 그룹에 대해 같은 방식으로 분기가 일어난다. 이 때문에 분기 과정 앞에 재귀적 이라는 말이 붙는다.
2. 가지치기 (pruning)
분기 작업이 모두 끝나면 이후에는 가지치기 작업이 일어난다. 가지치는 직관적의미 그대로 수 많은 가지로 분기하여 여러 leaf 노드를 가지고 있는 나무의 상위 노드에서 가지를 쳐내며 일부 데이터를 병합하는 과정이다.

순수 노드인 최하위 데이터들을 병합하여 상위 노드를 최하위 노드로 만들면 더이상 순수 노드가 아닐텐데 왜 이와 같은 작업을 하는것일까?
이유는 바로 과적합( Over-Fitting) 을 방지하기 위해서이다. 과대적합에 대한 내용은 또 별도로 정리할 예정이니 간단하게 설명하자면,
모델에서 과적합이 발생했다는 의미는 학습 데이터에 너무도 정교하고 세세하게 학습을 완료해서 학습에 쓰였던 데이터를 입력으로 받게 되면 높은 정확도/예측률 을 가지지만 비슷한 새 데이터에 대해서는 참담한 성능을 보이는 일반화 성능 이 꽝이 되었다는 의미이다.
가지치기의 과정도 분기 과정과 비슷하게 그 기준인 비용함수 (Cost Fucntion) 의 정도를 모든 분기점에 대해 조사한 후 손실이 가장 적은 분기점을 병합하는 식인데 TOP-Down 방식과 BOTTOM-Up 방식이 있다.
※ 참고 비용함수 (Cost Function) 의 표현 식
의사결정나무 모델 DT 에 대해
CC(DT) = E(DT) + α X L(DT)
- CC : Cost Complexity , 최종 비용
- E : Error , 해당 분기를 가지치기 하였을 때 , 트레이닝/학습 misclassification error
- α : 정규화 상수 ( 사용자에 의해 0.1~0.01 정도의 값으로 설정됨)
- L : Leaves , 모델의 최하위 노드의 수
 sklearn 라이브러리를 활용한 의사 결정나무
sklearn 라이브러리를 활용한 의사 결정나무
![]() 의사 결정나무 객체 생성
의사 결정나무 객체 생성
1
2
3
4
5
from sklearn.tree import DecisionTreeClassifier
from slkearn.tree import DecisionTreeRegressor
DT_C = DecisionTreeClassifier()
DT_R = DecisionTreeRegressor()
세부 옵션 :
-
criterion: 분기의 기준에서 쓰일 지표를 설정.- Classifier : ‘gini’ (지니 계수 , ‘entropy’ (엔트로피 지수)
- Regressor : ‘mse’ (mean-squared-error) , ‘mae’ (mean-absolute-error)
-
max_features: 트리 구성에 쓰일 설명변수의 수를 설정 (int, float, None, Auto) -
max_depth: 트리의 최대 깊이를 설정. -
min_samples_split: min_samples_leaf 와 혼동 주의. 현재 노드가 분기를 하기에 최소로 만족해야하는 샘플 수를 설정. 이 파라미터 값 이하의 수를 가진 노드는 분기 고려대상 바로 제외 -
min_samples_leaf: 분기가 일어날 때 하위 노드에 각각 최소로 포함되어야 하는 데이터 수를 설정. 만약 2라면 왼쪽 노드에도 최소 2개, 오른쪽 노드에도 최소 2개의 데이터가 포함되는 조건으로 분기가 일어나야함. -
random_state: 트리의 구성에서 무작위한 고려가 필요시 이용되는 파라미터. 예를 들어 max_feature 를 설정해 놓아서 각 분기마다 어떤 설명변수를 골라 criterion을 조사할지 , criterion을 조사했는데 완전히 동일한 둘 이상의 설명변수가 존재할 때 어느 설명변수를 기준으로 분할할지 등.
![]() 의사 결정나무 객체 학습
의사 결정나무 객체 학습
1
2
model_c = DT_C.fit(xdata,ydata,sample_weight)
model_r = DT_R.fit(xdata,ydata,sample_weight)
파라미터 세부내용
- xdata : 학습데이터의 입력값
- ydata : 학습데이터의 출력값
- sample_weight : optional 파라미터로 각 설명변수의 가중치 배열을 전달 가능. 분기 조사 과정에서 적용된다.
![]() 의사 결정나무 객체 예측/분류
의사 결정나무 객체 예측/분류
1
2
predict_C = model_C.predict(xtest)
predict_R = model_r.predict(xtest)
참고
예측 분류/값 에 대해 배열 형태로 반환받는다.
![]() 의사 결정나무 객체 평가
의사 결정나무 객체 평가
1
2
score_c = model_c.score(xtest,ytest,sample_weight)
score_r = model_r.score(xtest,ytest,sample_weight)
각 문제별 평가기준
-
분류(classification)- 단일 레이블의 경우 ACC (정확도) 를 기준으로 0~1 사이 값으로 평가
- 다중 레이블의 경우 각 레이블의 ACC 값의 평균으로 평가한다.
※ 다중 레이블은 ydata 의 컬럼이 2 이상인 데이터이다.
-
회귀(Regression)- R2 라고 많이 표현하는 결정계수를 평가 지표를 활용한다. 모든 데이터를 평균치로 예측하는 단순 모델(Zero-R)과 비교하였을 때 얼마나 개선된 성능을 보이는지를 구하는 결정계수의 값 또한 ACC 와 마찬가지로 0~1 사이의 값을 가진다.
![]() 의사 결정나무 기타 기능
의사 결정나무 기타 기능
-
 sklearn.tree 서브패키지의 plot_tree
sklearn.tree 서브패키지의 plot_tree
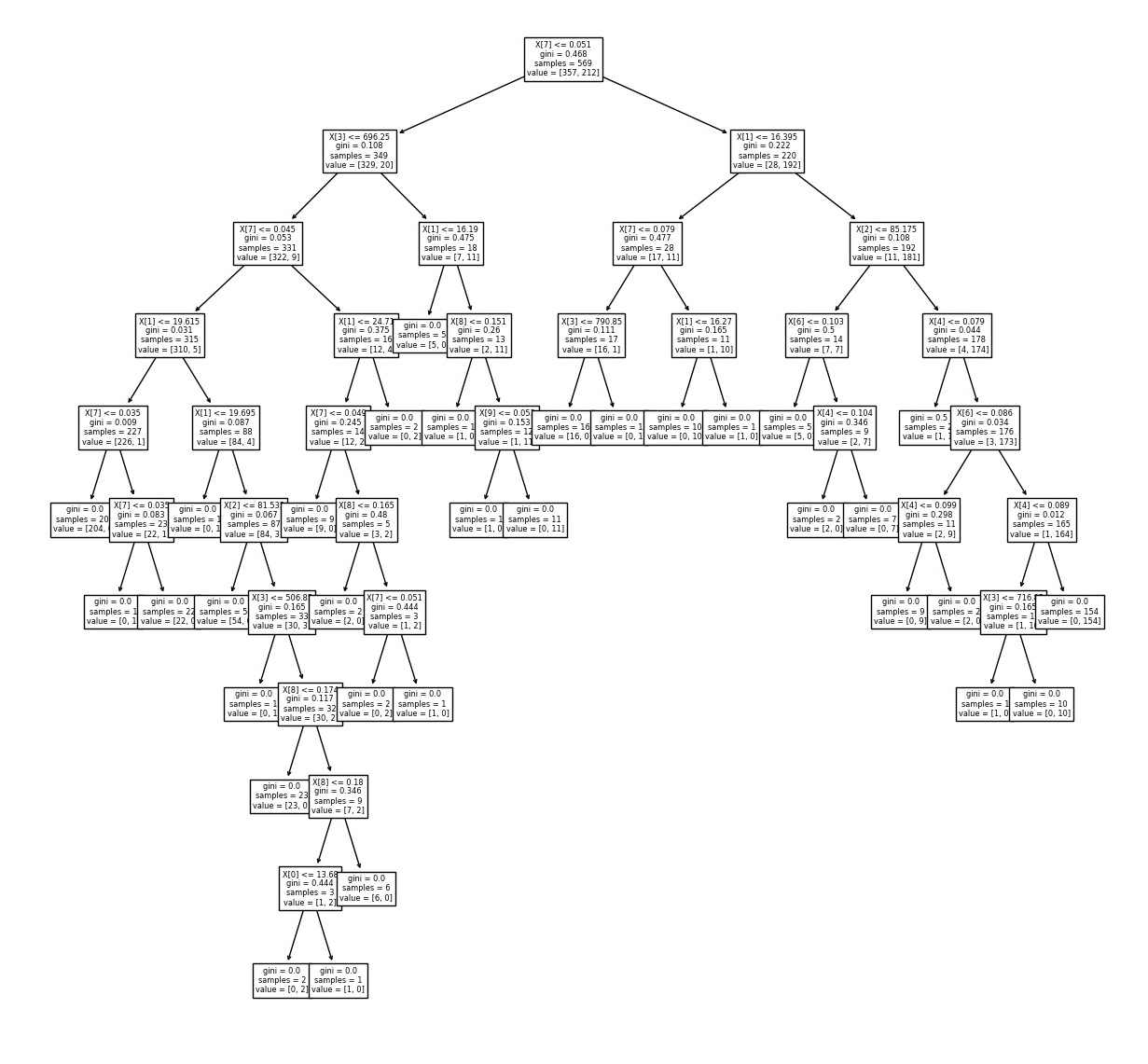
의사결정나무 객체를 전달하면 현재 학습이 완료된 객체의 모습을 시각화하여 볼 수 있다.
1
2
3
4
5
from sklearn.tree import plot_tree as pt
import matplotlib.pyplot as plt
fig , ax1 = plt.subplots(nrows=1)
fig.set_size_inches(20,20)
tree_picture = pt(model,ax=ax1)