Index
Ensemble 이란?
머신러닝/딥러닝에서 앙상블이란 여러 단일 예측(or 분류)모델을 하나로 엮어 더 좋은 성능의 복합 모델을 만드는 기법을 뜻한다.
사람으로 치면 조금 똑똑한 사람 여러명을 통한 집단 지성으로 아주 똑똑한 전문가 한 명보다 더 좋은 결과를 가져오는 상황 쯤으로 이해할 수 있다.
뛰어난 성능의 단일 모델도 물론 좋지만, 적당한 성능의 여러 단일 모델 조합하여 앙상블 모델을 활용하면 더 뛰어난 일반화 성능을 자랑하는 경우가 많기 때문에 지금까지도 이를 활용한 연구가 활발히 진행되고 있다.
Ensemble 의 3가지 유형
이러한 앙상블 기법에는 여러 종류가 있지만 가장 대표적이고 많이 쓰이는 유형은 3가지가 있다.
Voting
Bagging
Boosting
각 기법을 활용하는 대표 모델은 다음과 같다.
Bagging : Random Forest
Boosting : AdaBoost, Gradient Boost, XGBoost, LGBM
1. Voting
Voting 기법은 앙상블 기법 중 가장 간단한 기법으로 분류(Classification) 문제에서 활용된다.
“각각의 단일 모델들이 예측한 분류 중 가장 많은 비율을 차지한 레이블을 최종 결과로 예측한다” 가 바로 보팅 방식의 개념이다.
예를 들어 1,2,3 중 하나로 분류해야 하는 문제를 위해 10개의 단일 모델을 보팅 방식으로 앙상블 하였다고 가정하자.
각 모델들의 예측이 다음과 같다면,
1
2
3
4
5
6
7
1로 예측 : 2개 모델
2로 예측 : 5개 모델
3로 예측 : 3개 모델
1로 예측한 비율 => 0.2
2로 예측한 비율 => 0.5 (win!)
3로 예측한 비율 => 0.3
최종 결과를 2로 예측 하는것이 바로 Voting 이다.
이러한 Voting 기법은 크게 2가지 방식의 적용 방식이 존재하는데,
Hard Voting
- 위에서 예시로 든 상황처럼 각 모델들의 softmax(or logistic) 적용 값에서 가장 큰 값만 참고하여 비율을 계산
ex) A, B, C 모델의 softmax 적용 값이 다음과 같다면
A 모델 = {1일 확률: 0.7 , 2일 확률: 0.2 , 3일 확률: 0.1}
B 모델 = {1일 확률: 0.4 , 2일 확률: 0.3 , 3일 확률: 0.3}
C 모델 = {1일 확률: 0.0 , 2일 확률: 0.9 , 3일 확률: 0.1}
각 모델의 max 분류만 참고하여
“A번 모델 = 1이라 예측”
“B번 모델 = 1이라 예측”
“C번 모델 = 2이라 예측”
와 같이 생각하여 가장 비율이 큰
1을 최종 분류로 결정하는 방식으로 voting을 진행
Soft Voting
- hard voting 보다 조금 더 정교한 계산 방식으로, softmax(or logistic) 적용 값을 모두 참고하여 비율을 계산
ex) A, B, C 모델의 softmax 적용 값이 다음과 같다면
A 모델 = {1일 확률: 0.7 , 2일 확률: 0.2 , 3일 확률: 0.1}
B 모델 = {1일 확률: 0.4 , 2일 확률: 0.3 , 3일 확률: 0.3}
C 모델 = {1일 확률: 0.0 , 2일 확률: 0.9 , 3일 확률: 0.1}
각 모델의 softmax 값을 모두 참고하여
“1이라 예측한 softmax 값 총합 = 0.7(A) + 0.4(B) + 0.0(C) = 1.1”
“2이라 예측한 softmax 값 총합 = 0.2(A) + 0.3(B) + 0.9(C) = 1.4”
“3이라 예측한 softmax 값 총합 = 0.1(A) + 0.3(B) + 0.1(C) = 0.5”
와 같이 생각하여 가장 총합이 큰
2를 최종 분류로 결정하는 방식으로 voting을 진행
2. Bagging
Bagging 기법은 Random Forest 개념 정리 에서도 자세히 다뤘지만,
Bootstrapping + aggregating 의 합성 용어이다.
Boostrapping 이란 통계학 용어로, 전체 집합에서 무작위 복원추출을 통해 여러 부분집합을 만드는 행위를 말한다.
예를들어 [1,2,3,4,5] 라는 전체 데이터셋이 있을때 무작위 복원추출을 통하여 크기가 3짜리인 부분 데이터셋 [3,1,3] , [2,5,1] , [4,5,5] 등등을 만드는 것이 부트스트래핑이다.
이러한 행위의 목적은 전체 집합의 각기 다른 부분 집합을 통해 여러 모델들을 학습하게 되면 정답에 대한 편항을 증가시키는 효과가 있어 일반화 성능에 도움이 되기 때문이다.
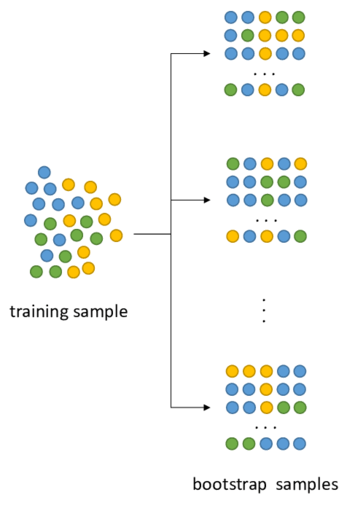
Aggregating 이란 ‘집계하다’ 라는 의미를 가진 광범위한 용어로 평균이나 최빈값 등을 도출하는 동작을 말한다.
Bagging 에서의 집계란 위의 Boostrapping 을 통해 생성된 각기 다른 데이터셋으로부터 학습한 여러 모델들의 아웃풋을 집계하여 최종 예측값/분류값을 도출하는 과정을 말한다.
학습의 목적이 Prediction / Classification 인지에 따라 집계하는 방식이 다른데, 가장 많이 활용되는 방식은 다음과 같다.
Prediction
Averaging : Bagging을 통해 엮인 각 모델들의 출력값의 평균을 최종 출력으로 사용한다.
if
Model_1 ==> 5.5
Model_2 ==> 7
Model_1 ==> 4.5
Final_output = (5.5 + 5 + 4.5)/3 = 5.0
Classification
데이터 성격에 맞는 Voting 방식을 택한다.
FYI, Random Forest 모델은 각 의사결정나무의 출력을 Hard-Voting을 통해 집계한다.
이러한 Bagging 기법은 Over-fitting에 빠지기 쉬운 단일 모델들에 적용하였을 때 효과있으며 다르게 표현하면
“편향이 작은 여러 모델” 들을 활용해 “분산을 줄이는” 앙상블 기법이라고 할 수 있다.
3.Boosting
Boosting 기법은 Bagging 과 비슷하면서도 다른 독특한 앙상블 기법이다. 그 공통점/차이점에 대해 한줄요약하면 다음과 같은데,
Boosting은 Bagging과 비슷하게 여러 모델들을 학습시키고 각 모델을의 출력을 Averaging , 혹은 Voting하여 최종 출력을 결정한다.
Boosting은 Bagging과 다르게 앙상블 되는 모델은 동일한 알고리즘 기반 모델이며, 각 모델들이 병렬적이 아닌 순차적으로 학습하고, 집계 시 각 모델의 출력에 가중치를 적용하여 집계한다.
즉, Boosting과 Bagging은 절차 껍데기는 같으나 각 단계의 동작은 다른 성격을 띈다. 다른 점을 하나씩 살펴보자면,
1.앙상블 되는 모델은 동일한 알고리즘 기반 모델이다.
- Bagging의 경우 랜덤 포레스트와 같이 동일 알고리즘 기반 모델을 앙상블 하는것도 가능하지만, 각 모델이 서로 의존적 관계가 아니기 때문에 다른 알고리즘 기반의 모델을 앙상블 하는것도 가능하다. (Ex. SVC + DecisionTree Classifier + BNaive Bayesian Classifer)
2.각 모델들이 병렬적이 아닌 순차적으로 학습한다.
- Bagging에서는 각 모델들이 Bootstrapping을 통해 생성된 부분데이터셋으로 학습하기 때문에
의존적 관계가 아니다라는 표현을 하였는데 Boosting에서는 각 모델들이 어떤 데이터를 통해 학습할지가 이전 모델이 학습하고 나서야 정해진다.
남자,여자 중 하나로 분류하는 예측작업을 위해 부스팅 앙상블을 활용하려면,
- 임의의 부분 데이터셋을 생성하여 단일 모델 하나(ex. DT)를 먼저 학습해본다.
1번의 모델의 분류별 예측률을 확인했더니남자레이블 예측이 더 저조하였다면1번에서의 학습 데이터셋에남자레이블 정보를 조금 더 추가한다.2번에서 보완된 데이터셋을 통해 다음 단일 모델을 학습해본다.2~3번의 과정을 반복한다.
이러한 방식으로 학습하기 때문에 순차적 학습 이라고 부른다.
Bagging , Boosting 방식의 차이를 그림으로 나타내면 다음과 같다.
3.집계 시 각 모델의 출력에 가중치를 적용하여 집계한다.
-
2번의 특징처럼 순차적 학습을 진행하게되면, 당연하게 이후에 학습하는 모델들이 더 좋은 성능을 보이므로 각 모델의 출력을 집계할 때 이런 성능차이를 고려하기 위하여가중치개념을 적용한다. - 참고 도서에서는 가중치를 모델의 정확도로 써서 예시를 들었는데,
예를 들어 남/여를 분류하는 작업을 하는 세 분류기의 정확도가 다음과 같고,
| 분류기1 | 분류기2 | 분류기3 | |
|---|---|---|---|
| 정확도 | 0.4 | 0.5 | 0.95 |
각 모델이 분류가 다음과 같을때,
| 분류기1 | 분류기2 | 분류기3 | |
|---|---|---|---|
| 분류값 | 남자: 0.7 , 여자: 0.3 | 남자: 0.8 , 여자: 0.2 | 남자: 0.1 , 여자: 0.9 |
랜덤포레스트 모델에서 소프트 보팅을 하였다면 분류기1의 0.7 , 0.3 이란 값이 그대로 쓰였겠지만,
Boosting 방식에서는 분류기1의 가중치(정확도)인 0.4를 곱한 값으로 집계하게 된다. (0.4X0.7 , 0.4X0.3)
따라서 최종적으로 각 레이블일 확률은 다음과 같이 집계되어
남자 : 0.4*0.7 + 0.5*0.8 + 0.95*0.1 = 0.775
여자 : 0.4*0.3 + 0.5*0.2 + 0.95*0.9 = 1.075
Boosting 모델의 최종 출력은 여자 레이블로 계산된다.
이러한 Boosting 기법은 under-fitting된 동일 단일 모델들에 적용하였을 때 효과있으며 다르게 표현하면
“분산이 작은 여러 모델” 들을 결합하여 “편향을 낮추는” 앙상블 기법이라고 할 수 있다.
참고자료
- 나의 첫 머신러닝/딥러닝 Chapter 4.6